1分钟完成最简Meta分析——系列(一)
我们直接演示Meta分析究竟在干什么。
为了确认“氟哌啶”治疗“精神分裂”疾病是否有效,我们需要整合多个RCT(随机对照实验)的研究证据。
1. 从多篇文献中提取如下数据
| 作者年份 | 用药有效人数 | 用药总人数 | 安慰剂有效人数 | 安慰剂总人数 |
|---|---|---|---|---|
| Arvanitis1997 | 25 | 50 | 18 | 51 |
| Beasley1996 | 29 | 47 | 20 | 34 |
| Bechelli1983 | 12 | 29 | 2 | 30 |
| Borison1992 | 3 | 12 | 0 | 12 |
| Chouinard1993 | 10 | 21 | 3 | 22 |
| Durost1964 | 11 | 19 | 1 | 15 |
| Garry1962 | 7 | 25 | 4 | 25 |
| Howard1974 | 8 | 17 | 3 | 13 |
| Marder1994 | 19 | 64 | 14 | 64 |
| Nishikawa1982 | 1 | 10 | 0 | 10 |
| Nishikawa1984 | 11 | 34 | 0 | 13 |
| Reschke1974 | 20 | 29 | 2 | 11 |
| Selman1976 | 17 | 18 | 7 | 11 |
| Serafetinides1972 | 4 | 14 | 0 | 13 |
| Simpson1967 | 2 | 16 | 0 | 7 |
| Spencer1992 | 11 | 12 | 1 | 12 |
| Vichaiya1971 | 9 | 29 | 0 | 29 |
Table 1. 从17篇文献中,整理了作者年份、用药有效人数、用药总人数、安慰剂有效人数和安慰剂总人数
2. 计算每篇文献中结果的p值
我们注意到,整理的各个组的数量,其实就是2x2四格表。以Table 1最后一行数据为例,可转换为如下2x2四格表。
| 组别 | 有效人数 | 无效人数 |
|---|---|---|
| 实验组 | a(9) | b(20) |
| 安慰剂组 | c(0) | d(29) |
n = a+b+c+d = 58
转换成四格表的目的,是为了计算p值。就是用数值结果来说明药物是否有效(实验组和对照组是否存在显著性差别)。对于四格表,可以使用卡方检验。
卡方值计算公式如下图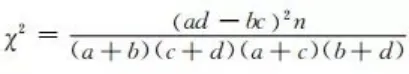
于是
分子是 (ad-bc)^2 n = (929 + 200 )^2 58 =3951018
分母是 (a+b)(c+d)(a+c)(b+d) = 29299*49 = 370881
chi_squar = 分子/分母 = 3951018 / 370881 = 10.65
再根据如下推理,可知p<0.01 具体是多少呢p=0.0010
对于四格表,只要计算出来的*卡方值大于3.841,说明p<0.05.卡方值大于6.635,说明p*值<0.01. Bruce Wayne (2024)
对每一篇文献计算卡方值,可以使用如下代码
from scipy.stats import chi2
strings = '''
Arvanitis1997|25|50|18|51
Beasley1996|29|47|20|34
Bechelli1983|12|29|2|30
Borison1992|3|12|0|12
Chouinard1993|10|21|3|22
Durost1964|11|19|1|15
Garry1962|7|25|4|25
Howard1974|8|17|3|13
Marder1994|19|64|14|64
Nishikawa1982|1|10|0|10
Nishikawa1984|11|34|0|13
Reschke1974|20|29|2|11
Selman1976|17|18|7|11
Serafetinides1972|4|14|0|13
Simpson1967|2|16|0|7
Spencer1992|11|12|1|12
Vichaiya1971|9|29|0|29
'''
for line in strings.split('\n'):
if len(line) >0:
a = int(line.split("|")[1])
b = int(line.split("|")[2]) - int(line.split("|")[1])
c = int(line.split("|")[3])
d = int(line.split("|")[4]) - int(line.split("|")[3])
numerator = (a*d - b*c)*(a*d - b*c)*(a+b+c+d)
denominator = (a+b)*(c+d)*(a+c)*(b+d)
chi_square = numerator / denominator
p_value = chi2.sf(chi_square,1)
print(numerator,denominator,chi_square,p_value)
于是表格变成这样。
| 作者年份 | 用药有效人数 | 用药总人数 | 安慰剂有效人数 | 安慰剂总人数 | p_value | ln(p_value) |
|---|---|---|---|---|---|---|
| Arvanitis1997 | 25 | 50 | 18 | 51 | 0.1351 | -2.0020 |
| Beasley1996 | 29 | 47 | 20 | 34 | 0.7937 | -0.2311 |
| Bechelli1983 | 12 | 29 | 2 | 30 | 0.0017 | -6.3605 |
| Borison1992 | 3 | 12 | 0 | 12 | 0.0641 | -2.7477 |
| Chouinard1993 | 10 | 21 | 3 | 22 | 0.0153 | -4.1804 |
| Durost1964 | 11 | 19 | 1 | 15 | 0.0019 | -6.2598 |
| Garry1962 | 7 | 25 | 4 | 25 | 0.3057 | -1.1850 |
| Howard1974 | 8 | 17 | 3 | 13 | 0.1768 | -1.7328 |
| Marder1994 | 19 | 64 | 14 | 64 | 0.3123 | -1.1636 |
| Nishikawa1982 | 1 | 10 | 0 | 10 | 0.3049 | -1.1878 |
| Nishikawa1984 | 11 | 34 | 0 | 13 | 0.0191 | -3.9573 |
| Reschke1974 | 20 | 29 | 2 | 11 | 0.0039 | -5.5359 |
| Selman1976 | 17 | 18 | 7 | 11 | 0.0331 | -3.4088 |
| Serafetinides1972 | 4 | 14 | 0 | 13 | 0.0368 | -3.3026 |
| Simpson1967 | 2 | 16 | 0 | 7 | 0.3276 | -1.1159 |
| Spencer1992 | 11 | 12 | 1 | 12 | 0.0000 | -10.0187 |
| Vichaiya1971 | 9 | 29 | 0 | 29 | 0.0011 | -6.8135 |
| abc | 80 | 300 | 50 | 500 | 0.0000 | -21.2078 |
3. 直接进行P值合并
按照fisher转换法进行计算
fisher_chi_square = -2 * sum( ln(p_value) )
自由度df = p值的个数 * 2
就是把全部的p值算一下对数再加起来,所得的和乘以(-2),即可得fisher卡方值。
fisher_chi_square = -2 *(-61.207) = 122.4068
df = 17 * 2 = 34
查表,或者使用python计算得到合并后的p值:6.5444e-12,也就是0.0000000000065444。这是个非常小的数,说明实验组和对照组有显著区别。证明了使用“氟哌啶”治疗“精神分裂”是有效的。
4. 总结
由多篇研究证据,汇总成更强的研究证据,就是Meta分析。
我们可以看到即使存在Beasley1996(p值为0.7937)以及Garry1962(p值为0.3057),Marder1994(p值为0.3123)这样的阴性结论,Meta分析仍然能汇总出有效的结果。